浮思特 | 探讨RC电路在逆变器设计中的应用与限制
不可能用简单的RC电路制作逆变器,我们注意到逆变器的重要性,因为这些设备在光伏系统中至关重要。不幸的是,重现一个完美的正弦波形(频率f0 = 50/60 Hz)非常困难,甚至是不可能的。这意味着必然存在与f0成倍的谐波,如果系统没有适当屏蔽,这些频率将产生电磁辐射,从而干扰其他传输/接收设备。
️积分电路
练习1:考虑施加在具有时间常数τ = RC的积分器电路上的以下输入:

其中:A = 10 V,τ0 = 1 s是特征时间,T = 8 s是周期。信号行为如图1所示。该输入是具有时间常数τ0的阻尼RLC电路的输出,该电路每8秒回到初始状态。因此,输入信号的频率为f0 = 1/8 Hz。
编写一个Wolfram机器程序,可以重构输出信号,区分τ ≠ τ0和τ = τ0的情况。用这样的设备能否制造逆变器?
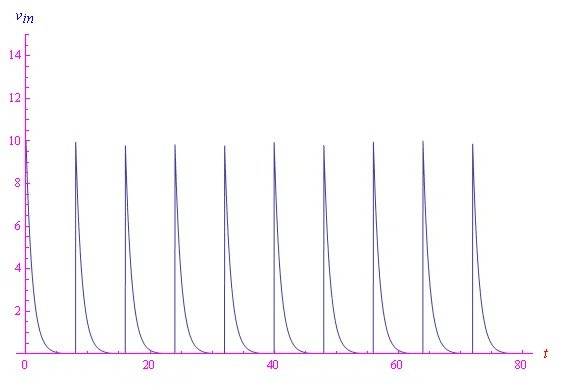 图1
图1
️解析解
展开全文这个练习的(表面)困难在于R和C值未知,但它们的乘积RC = τ(自由参数)。在之前的教程中,我们看到由基尔霍夫第二定律导出的微分方程包含时间常数τ和电阻值R,我们还必须添加电荷的初始条件,该条件可能是非零的(在这种情况下,电容器初始是充电的,因为它经历了先前的瞬态)。
通过解析地解决问题,在最后一步,即计算输出信号时,变量R消失,因此问题得到解决。然而,直接写出一个微分方程,其中未知函数不是电容器板上的电荷q(t),而是它们之间的电势差,即输出vout,这在计算上更简单。
这是由于电荷和电容器电容之间的线性关系:q = Cvout。我们邀请读者执行所有步骤,这些步骤并不复杂,以得出上述必须用显然的初始条件vout(0) = Cq(0) ≡ v(0)来解决的微分方程。
然而,有趣的情况是电容器初始未充电的情况,此时vout(0) = 0。这样,仅在初始值下此问题的唯一解在图2中给出,从中可以看出“积分器电路”这一表达的含义,因为输入通过一个积分进行处理。
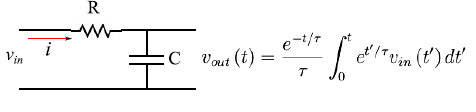 图2
图2
这里出现一个问题:当积分器电路的时间常数与输入的时间常数重合时,vout(t)的解析表达式不能使用,因为该表达式返回不确定形式0/0。如所周知,在这种情况下,微分方程在τ = τ0时被重写,然后进行积分。
在图3中,我们比较了输出的趋势与输入的趋势,对于以下τ值,四舍五入到小数点后三位:τ = 0.002,1.002,2.002,3.002 s。注意,第二个值接近τ0。我们因此看到,当τ趋近于零时,输出趋近于输入。在相反的极限(τ → +∞)中,输出趋近于完全为零的信号,正如预期中那样,因为在这个极限下,电阻或电容趋近于+∞。
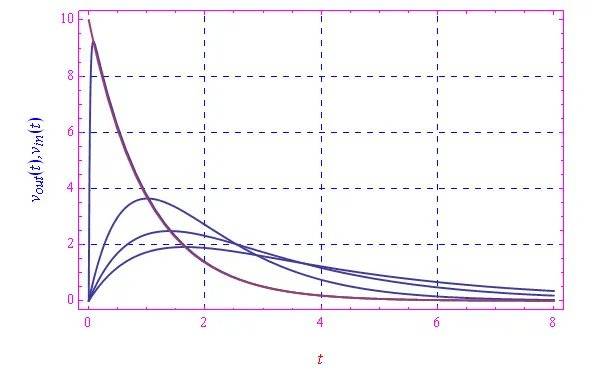 图3
图3
关于实现逆变器的可能性,答案是否定的,因为这需要一个更复杂的设备。从积分函数的符号(图2)可以看出这一点,该符号显然是正的。根据定积分的已知性质,我们得到这样的符号在[0, t]内定义了积分。
重置微分方程为τ = τ0并求解,我们得到图4和图5,其中我们首先在周期性区间比较vout(t)与vin(t),然后在[0, 80 s]内进行比较。
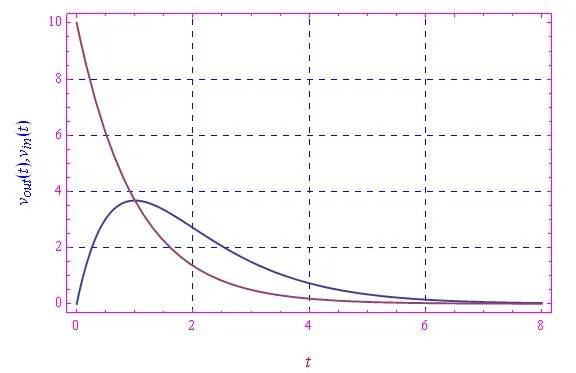 图4
图4
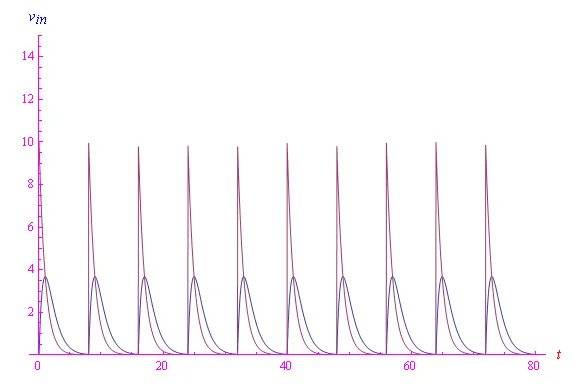 图5
图5
️使用Mathematica的解法
一旦设置了适当的Wolfram机器微分方程,将τ作为自由参数,如果我们尝试绘制τ = τ0的解,内核将尝试通过执行除以0的操作来消除不确定形式0/0,随之而来的是错误消息。我们可以将WM分成两个不同的WM,一个用于τ ≠ τ0,另一个用于τ = τ0,但更优雅的做法是设置一个IF循环,如图6的屏幕截图所示,我们突出了相应Mathematica代码的一些重要方面。
 图6
图6
关于整个代码的PDF格式,我们参考文献1。首先,不能使用延迟赋值“:=”,这告诉内核仅在新输入调用时确定相应的表达式(函数、指令、其他)。这种类型的赋值用于递归程序和缓存技术,但在处理导数等时会产生问题。
例如,如果我们使用延迟赋值来确定某个函数f(x)的导数,然后询问在某个特定点x0的导数值,内核首先在f(x)的解析表达式中替换x0的值,然后再计算导数,随之而来的是明显的错误消息(实际上应该为零,因为常数的导数为零)。可以使用强大的Evaluate指令,或者更简单地使用直接赋值“=”。
对于微分方程而言,情况更复杂,仅使用直接赋值是不够的,而需要插入Evaluate,我们在后缀表示法中使用它以避免括号的过度使用。代码被正确解释,我们通过与解析结果进行比较进行了若干检查。
关于IF循环,众所周知,它是传统编程语言的典型特征,在Mathematica中,其语法如下(*之间的字符串是被内核忽略的注释条目):
If[ (*condition*) expr, (*then*),
t (*else*) p
]
也就是说,如果expr为真,内核执行t,否则执行p。例如:
复制In[1]=test[x_] := If[ x^3 > 14,
Print[“正确答案。结果为:” , x^3], Print[“错误答案”]
]
In[2]=test[2]
错误答案
In[3]=test[3]
错误答案
正确答案。结果为:216
️结论
尽管“封装”软件如Mathematica/Maple、Maxima等表现得像一个黑箱,因为它们不允许直接访问代码,但在许多应用中,它们极其灵活,允许用几行代码解决复杂问题(这种情况是传统编程语言如Fortran或C无法实现的)。
浮思特科技深耕功率器件领域,为客户提供IGBT、IPM模块等功率器件以及单片机(MCU)、触摸芯片,是一家拥有核心技术的电子元器件供应商和解决方案商。
️END
️关于我们:
️深圳市浮思特科技有限公司 成立于2008年,位于深圳市南山区,是一家专业从事️功率器件、半导体元器件供应和应用方案开发业务的企业,长期并将持续追求核心技术,曾被评选为深圳高新技术企业,广东省专精特新企业。公司长期专注4大产品线:️新能源、电动汽车及充电桩、家用电器、触控显示,且均已有不同程度的方案沉淀,为客户提供从方案研发到选型采购的一站式服务。



